
검은 점끼리도 한 자리씩 차이난다.
0101=a'bc'd 와 1101=abc'd 를 묶으면 a가 사라져서 bc'd 가 남고,
1101=abc'd 와 1111=abcd 를 묶으면 c가 사라져서 abd가 남는다. (kmap의 특징)
kmap의 특징은 인접한 셀들 사이에 하나의 요소만 차이난다. 강조!
| a | b | cin | cout | sum |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Cout의 Kmap =


1의 값을 묶어야 하는데, 묶는 크기는 2의 제곱수 밖에 되지 않는다.
이때 최대한 크게 묶으면서 최소의 갯수로 묶어야한다.
6, 7, 8은 3개이므로 한번에 묶을 수 없고, 이때는 34, 67, 78로 묶어야 최적의 값이다.
Sum의 Kmap =

최대한 크게 묶으면서 최소의 갯수로 묶어야 하는데,
4개가 서로서로 2개 이상이 차이가 나기 때문에, 각각 1개씩 4개의 써클이 최적의 값이다.

1. truth table 등 을 이용하여 minterm을 확보.
2. 입력 변수에 따라서 kmap을 채운다.
3. 모든 1들만 덮는다. 서클의 크기를 최대로하고(2의 제곱수) 개수를 적게해서 묶어서
or 시키면 최적화된 디자인을 뽑아낼 수 있다.








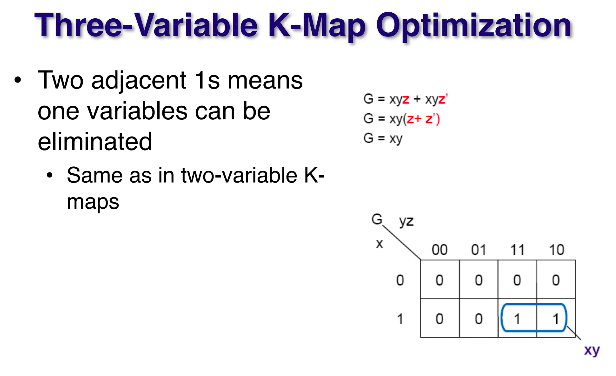
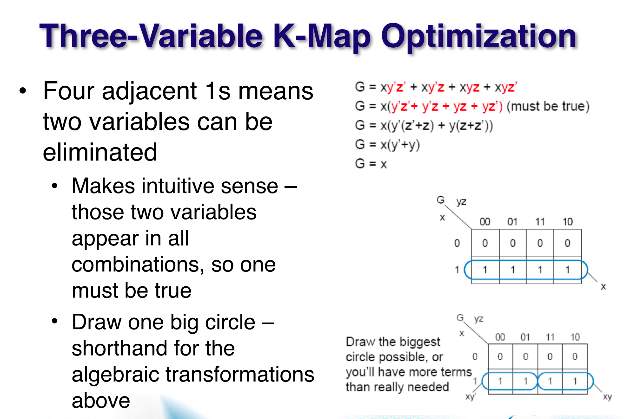
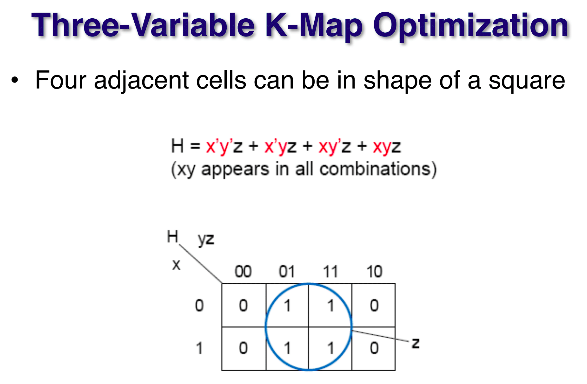
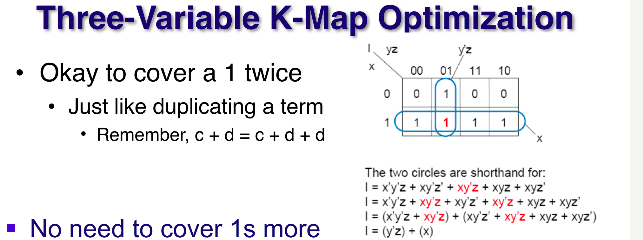
(kmap 방 순서를 1 2 3 4 , 5 6 7 8 로 정한다고 가정한다.)
최적화를 할라면 가장 크게, 써클의 갯수를 적게 할라면 5678을 묶고 26을 묶으면 된다.
5678을 묶고 2만 묶어도 되는데, 2번방 하나보다 26방이 한개의 요소가 더 적다.(2번 = x'y'z, 26번 = y'z)
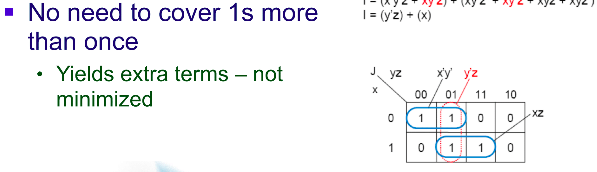
12를 묶고 67을 묶어서 다 됐는데, 굳이 26을 추가로 넣지 않는다. 불필요한 써클은 넣지 않는다.
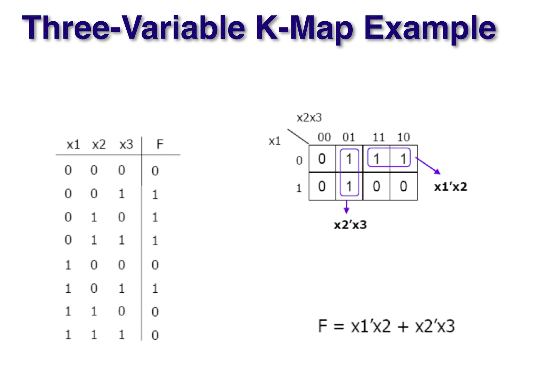
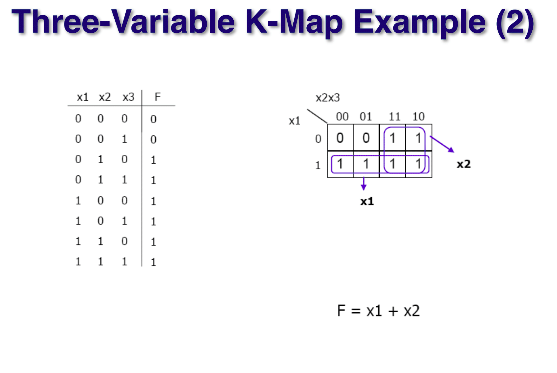
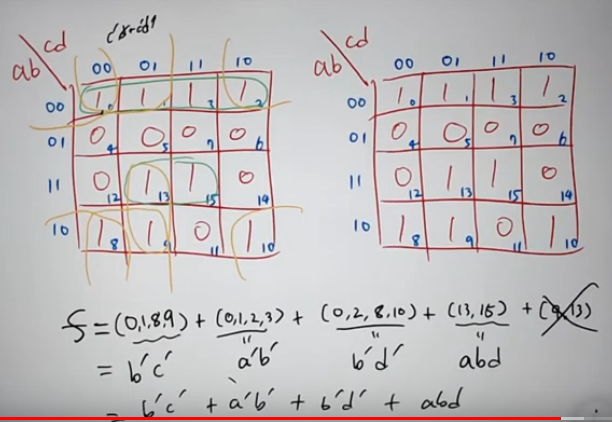
위의 예시에서 1을 크게 묶고, 갯수를 적게 할려면
f = (0,1,8,9) + (0,1,2,3)+(0,2,8,10)+(13,15) 로 하면 된다.
근데 (9,13)은 굳이 추가할 필요가 없다. (13,9)는 (0,1,8,9)와(13,15)에 포함되기 때문이다.
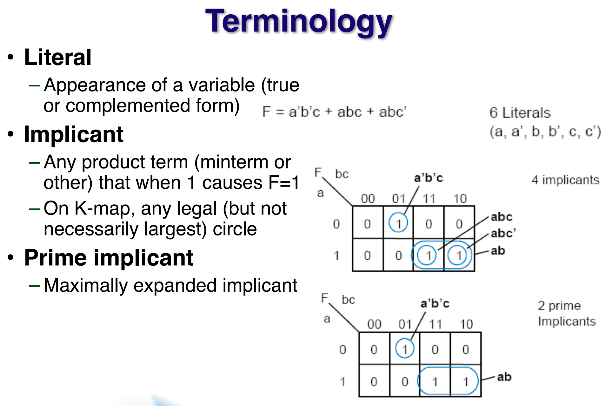
Literal : 입력 원소와 입력원소의 인버트된 원소의 구성요소
Implicant : minterm과 다르게 변수의 개수가 자유롭다. ( a, ab, abc, abc' 등 Implicant 이다.)
Prime implicant : Implicant에서 크게 묶은 것이라고 생각하면 된다.
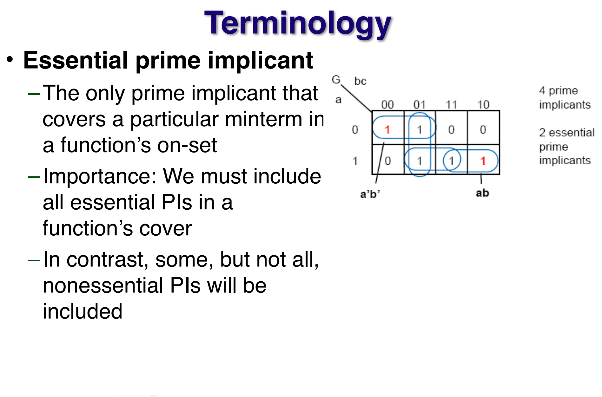
Essential prime implicant = Epi
출력값이 1인 셀이 있는데(빨간색으로 표현된 1), 서클로 묶여지는 갯수가 단 하나인 경우
ex) abc=000인 m0 는 출력값이 1이고 서클로 묶여지는게 (m0,m1) 단 하나이다.
반면 abc=001인 m1은 m0과 m6으로 2개의 써클로 묶어줄수 있기 때문에 Epi가 아니다. = Non-Epi = nepi
식을 구성할 때에는 Epi를 먼저 구성하는게 좋다.
따라서 G = (m0m1) + (m8+m7) = a'b' + ab 로 시작한다. 그다음 m6가 남아 있으니
G 식에 (m1m6) or (m6m8) 을 더해주면 끝이다.
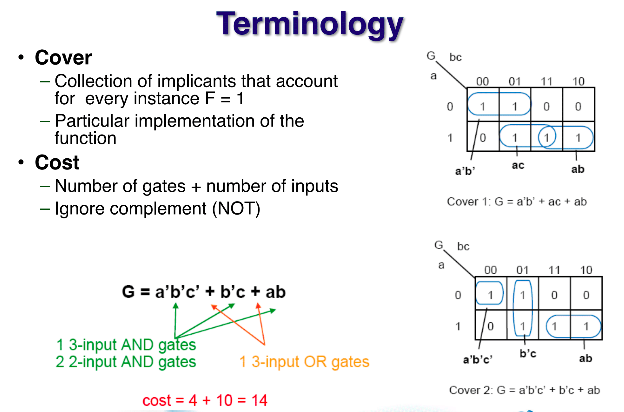
cover : 1만 구성되게 덮는다 = 1로만 구성되는 써클을 만든다. = 써클의 집합
cost : 예로들어서 설명하겠다. abc + bc 라고 주어지면
abc는 3개의 input이 들어가서 a
nd가 되서 output값 하나가 나온다. = 3+1 = 4
bc는 2개의 input이 들어가서 and가 되서 output값 하나가 나온다. = 2+1 = 3
방금 계산에서 나온 2개의 output값이 or이 되서 output값 하나가 나온다. = 2+1 = 3
그래서 총 4+3+4=10 이라는 cost가 나온다.
위 그림에서 Cover1에서는 3+3+3+4 = 13이 나오고,
Cover2는 4+3+3+4 = 15가 나온다. 이때는 "C1이 C2보다 cost 관점에서 최적화된 회로"라고 말할 수 있다.

- 최대한 확장된 서클을 찾는다.
- 무조건 들어가야 되는 서클(epi가 포함된 서클) 찾는다.
(ex : 5개의 서클 = 5개의 prime implicants 가 있다고 쳤을때 넣고빼고 하면서 cost가 얼마인지 알아 볼때,
경우의 수는 2^5승이 나오는데, 만약 3개의 서클이 epi라고 확인이 되면 경우의 수는 2^2승이 나온다.
- epi인 서클을 제외하고 nepi가 존재한다면 전수조사를 해서 비교해보는 방법도 있고,
nepi중 하나를 선택해서 넣고빼고 = cover에 사용할까를 가정하면, 여기에 붙어있는 다른 nepi들이 epi로 바뀌는 경우도 있다.
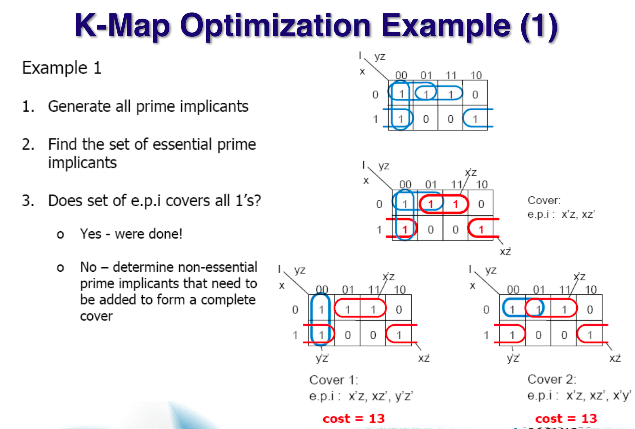
1. 모든 prime Implicants를 찾는다.
2. epi를 찾는다. (빨간색 서클)
3. npei인 m0을 여러 커버에 넣어보고 cost를 비교해본다. (예시1은 cost가 같은 다른 디자인이다.)
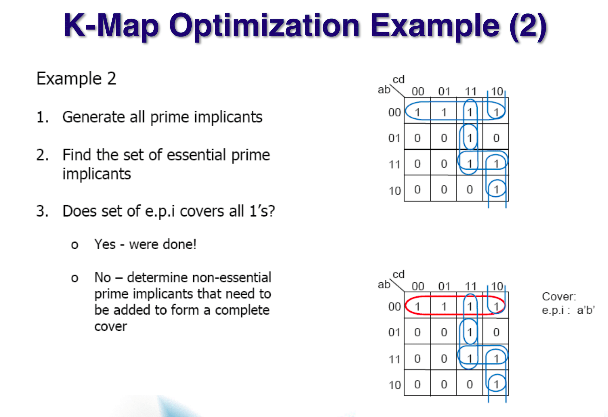
모든 prime Implicants를 찾아 봤는데 7개의 서클이 나온다. 그중 최대한 크게, 최소의 갯수로 해야된다.
epi는 m0m1m3m2 1개이다. 나머지 서클을 가지고 넣을지 말지 판단하면서 cover를 찾는다.
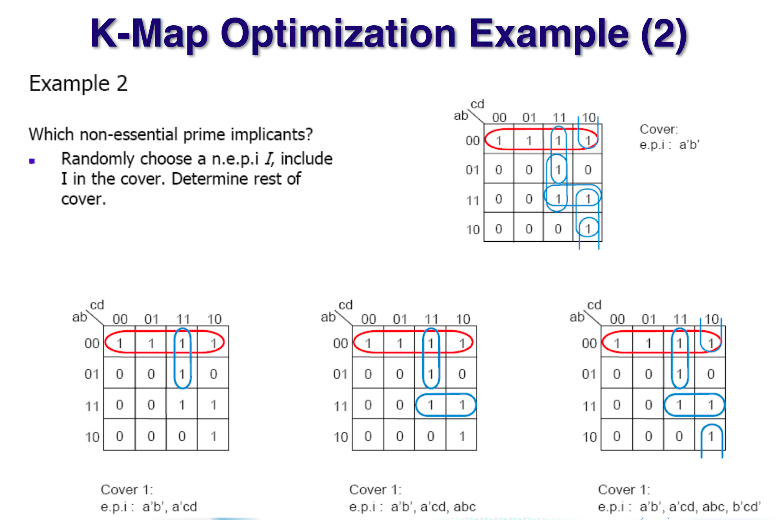
예시2-1은 m3m7을 사용한다고 가정했을때, 나머지를 가지고 최적화된 서클을 찾아나가는 예시이다.
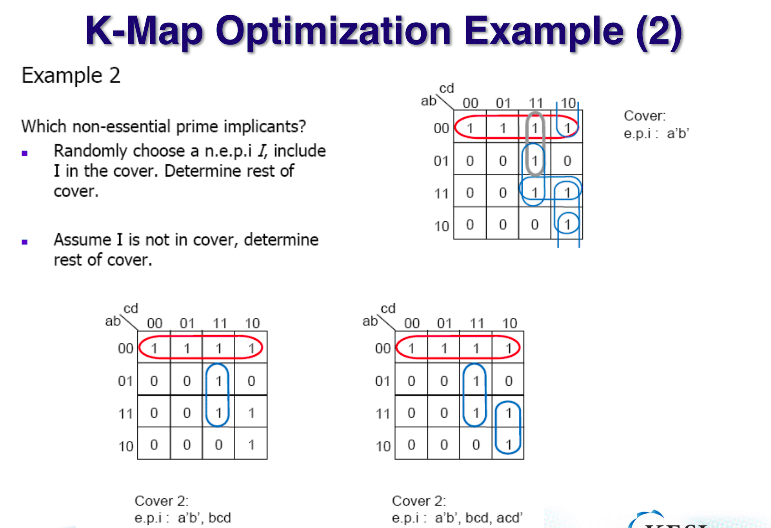
예시2-2는 m3m7이 아니라 m7m11을 선택했을때, 나머지를 가지고 최적화된 서클을 찾아나가는 예시이다.
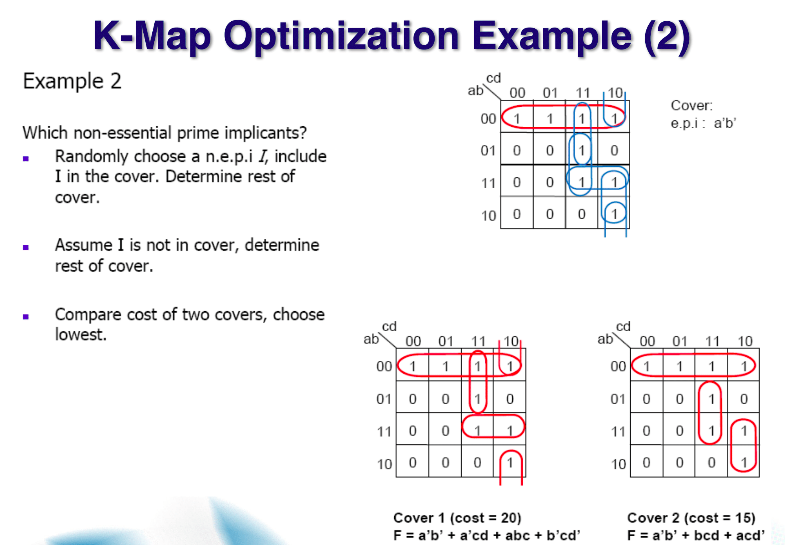
예시2-1 과 예시2-2를 통해서 cost를 비교해본다. 예시2-2 처럼 했을때, 최적화된 식이 나온다.(cost가 낮다.)
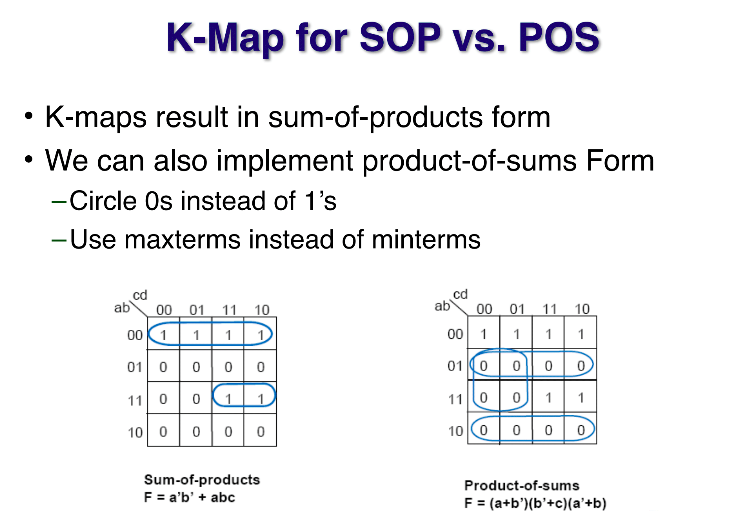
SOP로 풀었을 때 보다 POS로 풀었을 때 낮은 cost로 풀릴 수 있다. kmap에서도 적용이 된다.
F에 대해서 SOP의 kmap,POS의 kmap을 구성하고 cost를 비교해본다.
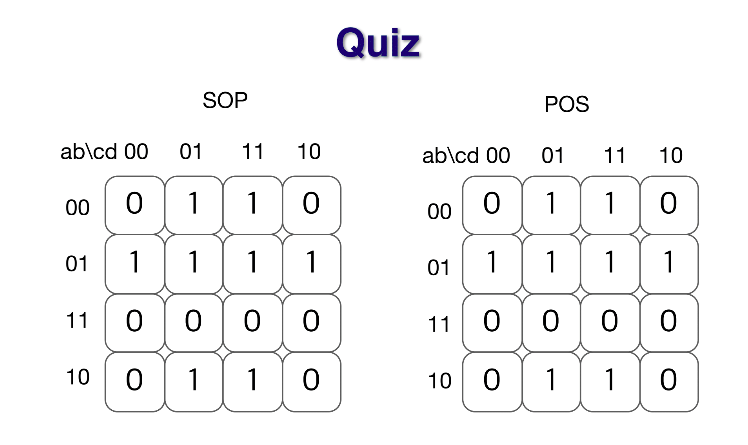
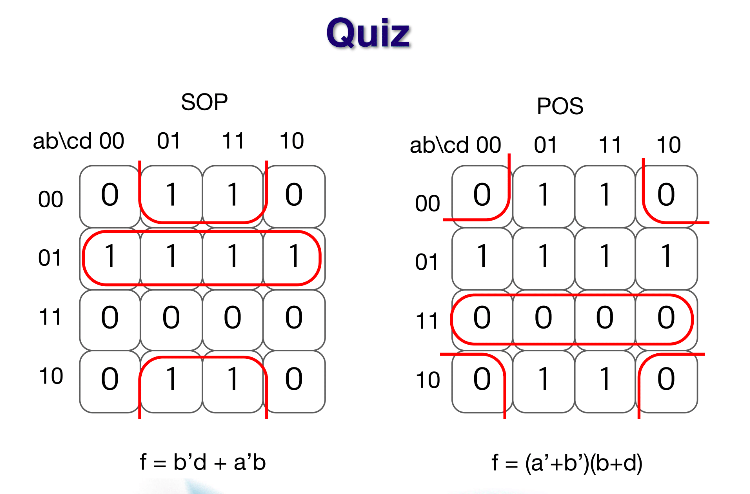
'Study > Digital Logic Design' 카테고리의 다른 글
| 논리회로설계 5-2 (0) | 2022.04.07 |
|---|---|
| 논리회로설계 5-1 (0) | 2022.04.07 |
| 논리회로설계 4-3 (0) | 2022.04.03 |
| 논리회로설계 4-2 (0) | 2022.03.28 |
| 논리회로설계 4-1 (0) | 2022.03.22 |