SOP와 POS의 관계

a, b가 주어지고 결과 값(f) 0101의 truth table을 한번 보자.
| a | b | f | f' |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
그러면 minterm과 maxterm의 식을 구할 수 있다.
| minterm식 | maxterm식 | ||
| m0 | a'b' | M0 | a+b |
| m1 | a'b | M1 | a+b' |
| m2 | ab' | M2 | a'+b |
| m3 | ab | M3 | a'+b' |
F
= m1 + m3 = a'b + ab
= M0 * M2 = (a+b) * (a'+b)
라고 말할 수 있다.
f의 식에서 m+m3과 M0+M2는 듀얼인 것 같고,
위의 표에서 m 식과 M 식은 인버전(') 관계 같다.
F = (F')' 을 알아봐야 한다.
F'의 결과 값은 1010 이고, F' = m0 + m2 = M1 * M3이다.
그러면 F = (F')' = (m0 + m2)'라고 말할 수 있다.
(m0 + m2)' = m0' * m2' = M0 * M2 가 된다. (F'을 m0+m2 캐치하는 것이 핵심이다.)
만약 F = m1+m3이라고 F' = (m1+m3)'을 한다면 본래식으로 바로 돌아오기 때문에 위 핵심을 기억하자.
추가 설명)
F의 SOP에서 m1, m3에 대해서 M1, M3을 구하는 게 아니라
F를 인버전 시키면 F'=1010이 되니까 이때의 sop = m0, m2를 가지고 M0, M2를 알아본다는 말이다.
ex)
| a | b | f | f' |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
만약 f=0100라고 한다면
f = (a'b = m1) = (f')' = (m0+m2+m3)' = M0 * M2 * M3
즉 m1 = M0*M2*M3이다.
Self Dual
f = a'b+ab = b 식은 함수이지, 항등식이 아니다. 듀얼을 막 취하면 안 된다.
그러나 fd(f의 dula)을 구할 건데,
f = (a'+b)*(a+b) = a'b+ab+b = b 가 나온다.
f의 결과도 b이고, fd의 결과도 b이다.
이는 Self dual이라고 한다.
ex) f = xy + yz + zx 이 있다고 하자.
항등식인지는 모르겠지만 fd를 한번 구해보자.
fd = (x+y)(y+z)(z+x)
= (xy+y+xz+yz)(z+x)
= (y(1+y+z)+xz)(z+x)
= (y+xz)(z+x)
= xy + yz + xz
듀얼을 취했더니 f의 식이 나온다. 이를 Self dual이라고 한다.
self dual의 정의)
1. 모든 함수는 self dual이 되는 건 아니다.
2. minterm의 개수와 maxterm 개수가 같아야 한다.
3. 배타적 관계여야 한다.( xyz & x'y'z' , x'yz & xy'z')
위의 f의 식은 입력값이 3개이니 2^3=8줄이 나온다.
self dual을 가능하게 하려면 f의 결과 값 중, 1의 개수가 4개여야 하며
| x | y | z | f | |
| 0 | 0 | 0 | 0 | m0 |
| 0 | 0 | 1 | 0 | m1 |
| 0 | 1 | 0 | 1 | m2 |
| 0 | 1 | 1 | 0 | m3 |
| 1 | 0 | 0 | 1 | m4 |
| 1 | 0 | 1 | 0 | m5 |
| 1 | 1 | 0 | 1 | m6 |
| 1 | 1 | 1 | 1 | m7 |
m3과 m4 , m2와 m5, m1과 m6, m0과 m7이 인버전 관계이며 (4쌍이 나온다.)
이를 배타적 관계라고 한다.(정의 3)
만약 self dual이 돼야 한다면 위의 관계에서 4쌍이 각각 0과 1의 결과 값을 가져야 하며,
이 함수에서 self dual의 개수를 구하러면 2^4이 된다.
(m3 | m4중에서 01 or 01) : 2가지 * (m3 | m4중에서 01 or 01) : 2가지
* (m3 | m4중에서 01 or 01) : 2가지 * (m3 | m4중에 01 or 01) : 2가지 = 2*2*2*2 = 16가지
self dual의 갯수 일반식 : 2의(2의 n-1승) 승 = 2^(2^(n-1))
(n = 입력 개수)
Karnaugh Maps(k map)

4*4 kmap
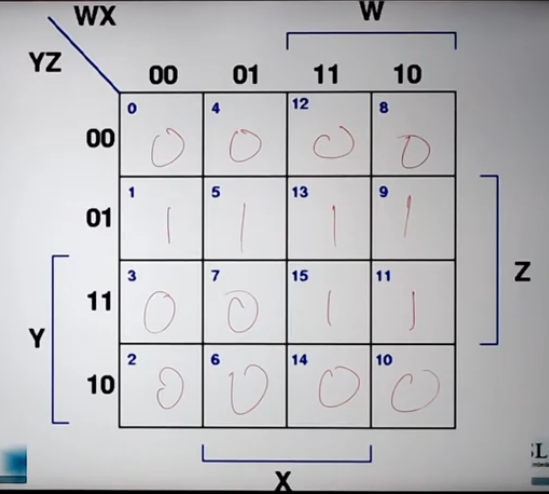
m0 = w'x'y'z', m1 = w'x'y'z, m3 = w'x'yz, m2 = w'x'yz', m4 = w'xy'z', m15 = wxyz
m0 + m1 = w'x'y' : 0000과 0001
m0 + m4 = w'y'z' : 0000과 0100
m0 + m2 = w'x'z' : 0000과 0010
m0 + m15는 최적화가 되지 않는다. : 0000과 1111
인접하고 있는(한 칸 차이) m의 식들은 : w x y z 중 한 개가 차이 나서 최적화가 된다. (하나씩 차이 난다.)
만약 위 그림에서 f의 식을 구할 때, minterm의 개수가 6개를 구해야 한다.
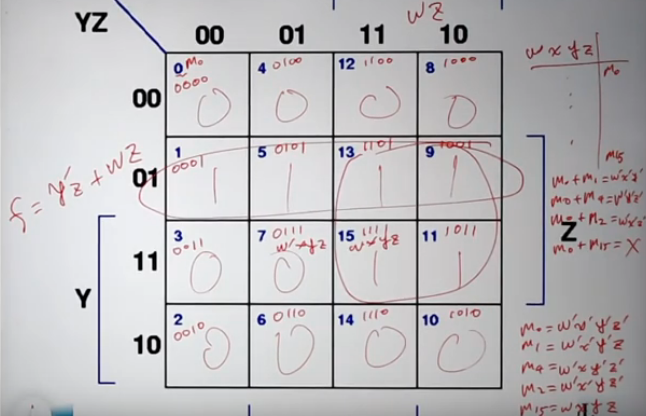
이 k map에서 1 번식 : m1, m5, m13, m9를 묶고,
2 번식 : m13, m15, m9, m11을 묶으면 결과 값 1이 다 묶인다.
1 번식은 WX의 값은 0과 1로 계속 바뀌고, YZ값이 01로 고정이니 Y'Z
2 번식은 W는 1로 고정이고 X는 0과 1로 바뀌고, Y는 0과 1로 바뀌고, Z는 1로 고정이니 WZ
즉 F = Y'Z + WZ이다.
특징)
서클을 묶을 때는 1,2,4,8... 2^n승 개로 묶어야 한다.
방향이 0 1 3 2 순서이다 = 00 01 11 10 (x축 y축 둘 다)
kmap의 크기는 4*4가 적당하다. 그 이상은 3차원이기 때문에 힘들다.
도넛 모양이기 때문에(다음장에 있다.) m0과 m8도 한자리 차이나고, m12와 m14도 한자리 차이이다.
'Study > Digital Logic Design' 카테고리의 다른 글
| 논리회로설계 6-1 (0) | 2022.04.07 |
|---|---|
| 논리회로설계 5-1 (0) | 2022.04.07 |
| 논리회로설계 4-3 (0) | 2022.04.03 |
| 논리회로설계 4-2 (0) | 2022.03.28 |
| 논리회로설계 4-1 (0) | 2022.03.22 |