



논리곱들의 합 형태인 SOP인 폼에서도 NAND 로직 게이트만 가지고 구성할 수 있다.
(x1*x2) + (x3*x4*x5)인 형태에서 이중부정을 취하면 = ( (x1*x2)' * (x3*x4*x5)' )' 이 된다.

논리합들의 곱 형태인 POS인 폼에서도 NOR 로직 게이트만 가지고 구성할 수 있다.
(x1+x2) * (x3+x4+x5) 인 형태에서 이중부정을 취하면 = ( (x1+x2)' + (x3+x4+x5)' )' 이 된다.




이거는 truth table로 처리하기에는 2^8의 줄 수가 나오기 때문에 힘들다.
그래서 사람의 직관적으로 본다.(일반화 하기에는 어렵다. 마치 트릭)

아주 대표적인 컴비네이션 로직 중 하나이다. 7개의 입력에서 뭘 넣냐에 따라 값이 바뀐다.

w, x, y, z 값이 2진수로 주어지면 디코딩을 해 얼마인지 알고, a~g의 값을 이용하여 디스플레이로 나타내는 구조이다.
이 디스플레이는 0~9까지 출력하기 때문에 4비트(2^4승)으로 표현이 가능하다.(2^3승 은 8까지 밖에 표현 안됨.)
그러나 10부터 15까지는 필요가 없다. = 어떻게 써도 상관없다. = Don't care condition
이 자유도를 이용해서 더욱 최적화가 가능하다.
예시 5-2를 보면 입력값에 따라서 출력 값이 어떤지 truth table을 이용해 만든 그림이다.
(가로축을 보는 게 아니라 세로축을 봐야 한다. = truth table 이용할 때는 필수다. 앞에도 많이 그래 왔음.)
0~9까지 총 10가지의 입력이 들어올 때, a는 1011011111 = 8번을 켜면 된다.
a가 언제 켜지는지 알기 위해 Minterm(SOP)을 구하려고 하니, 예시 5-2의 밑처럼 a의 식이 길게 나온다.
이때는 Maxterm(POS)을 이용하면(a가 안 켜질 때, a=0) a의 식을 줄일 수 있다.
10부터 ~ 16까지의 입력값에 대해서는 결괏값은 아무 상관없기 때문에 a의 값을 1로 설정한다.
따라서 a의 0의 값은 총 2개라고 말할 수 있다.
a의 Maxterm = (w+x+y+z')*(w+x'+y+z)
c도 Maxterm을 쓰면 편해 보인다 c의 Maxterm = (w+x+y'+z)
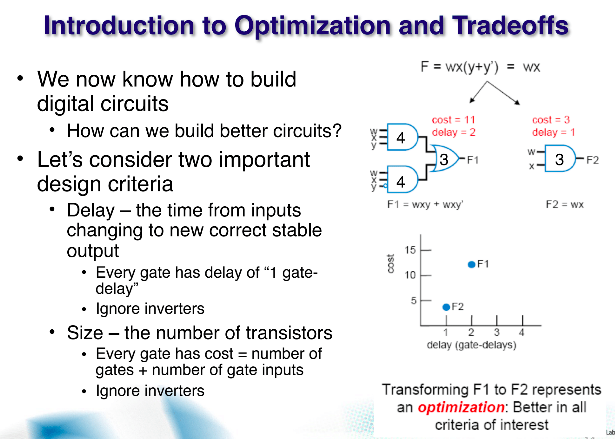
F1과 F2는 기능적으로는 같다.
F1을 최적화를 한 식은 F2가 되고, cost(핀 카운트)와 delay(가장 길게 거치는 길)가 낮아졌다.
그래프 상으로도 원점에 가까워졌다. 이는 최적화라고 말할 수 있다.

x축, y축으로 두쪽 다 개선이 되는 방향으로 가야 하는데, G1과 G2는 하나를 이루면 다른 하나는 이루지 못한다
이는 Tradeoff 관계라고 말할 수 있다.(Pareto - optimal : 하나가 좋아지면 반대쪽 하나는 나빠진다. 둔다는 안된다.)

G3이라고 예시를 들자면, G3는 pareto-optimal이 아닌 구역이다.
g3에 g1-g2그래프로 가는 걸 최적화한다라고 말하고,
pareto-optimal구간에서 왔다 갔다 하는 걸(g1, g2) tradeoff라고 말한다.


최적화하는 여러 방법이 있다.
1. 같은 것으로 묶는다.
2. x+x=x의 Duplicate성질을 이용한다.
3. 묶을 수 있을 때까지 묶는다.
ex)
LHS = a'b'+a'b+ab , RHS = a'+b
a'b'+a'b+ab
= a'(b'+b)+ab
= a'+ab
= (a'+a)*(a'+b)
= a'+b = RHS
그럼 이 식은 항등식인가? 맞다. 방금은 항등식임을 증명했다.
항등식이면 Dual을 취할 수 있다.
만약 이 식이 항등식인지 모른다면, dual식이 항등식이면 본래 식도 항등식임을 알 수 있다.
Dual)
LHS = (a'+b')(a'+b)(a+b) , RHS = a'b
= (a'+(b*b'))(a+b)
= a'(a+b)
= a'*a + a'*b
= a'b = RHS , 즉 항등식이다.
'Study > Digital Logic Design' 카테고리의 다른 글
| 논리회로설계 6-1 (0) | 2022.04.07 |
|---|---|
| 논리회로설계 5-2 (0) | 2022.04.07 |
| 논리회로설계 4-3 (0) | 2022.04.03 |
| 논리회로설계 4-2 (0) | 2022.03.28 |
| 논리회로설계 4-1 (0) | 2022.03.22 |